Επιστήμη και Τέχνη: Η περίπτωση της φράκταλ γεωμετρίας

Γράφει ο Βασίλης Κωνσταντούδης // *

Ινστιτούτο Νανοεπιστήμης & Νανοτεχνολογίας, ΕΚΕΦΕ Δημόκριτος

Ι. Εισαγωγή : Προς μία θετική ανάδραση Επιστήμης και Τέχνης

Συνήθως η Επιστήμη συνδέεται με τη λογική, το πείραμα, την συστηματική παρατήρηση και σκέψη, τις μαθηματικές εξισώσεις, την αντικειμενοποίηση του κόσμου. Αντίθετα, η Τέχνη παραπέμπει στη φαντασία, τη δημιουργία, την ελευθερία, την πρόκληση, την ομορφιά, την προσωπική έκφραση. Ως εκ τούτου, συχνά θεωρούνται δύο εντελώς διαφορετικά πεδία της ανθρώπινης ζωής και δημιουργίας χωρίς αλληλεπιδράσεις και δυνατότητες συνέργειας. Είναι όμως έτσι; Όντως μιλάμε για δύο διαφορετικούς κόσμους χωρίς επαφή και διασυνδέσεις; Ένα απλό ξεφύλλισμα των πρακτικών των προηγούμενων συνεδρίων της ΕΕΦ για τις σχέσεις Επιστήμης και Τέχνης ή του τελευταίου βιβλίου του A. Ι. Miller “Colliding worlds” (W.W. Nordon and Company, Inc., 2014), αρκεί για να υπονομεύσουν την πρώτη αυτή θεώρηση. Επιστήμη και Τέχνη μπορεί να αποτελούν δύο διακριτές δραστηριότητες του ανθρώπου χωρίς όμως να είναι ούτε ανεξάρτητες ούτε απομονωμένες. Τόσο στο παρελθόν όσο και πολύ περισσότερο στο παρόν, μπορούν να ανιχνευθούν αλληλεπιδράσεις και διασυνδέσεις που πολλές φορές δεν είναι εμφανείς.

Στην εισαγωγή αυτού του σύντομου άρθρου, θα παρουσιάσουμε μία όψη αυτής της αλληλεπίδρασης που σχετίζεται με το πρόβλημα της υποκειμενοποίησης της επιστημονικής γνώσης και σκιαγραφεί το γενικό πλαίσιο στο οποίο κινούμαστε όσον αφορά το διάλογο της επιστήμης με την τέχνη, ενώ στις υπόλοιπες παραγράφους, θα δούμε την συμμετοχή και διαμεσολάβηση της φράκταλ (μορφοκλασματικής) γεωμετρίας σε αυτόν τον διάλογο.

Όπως αναφέραμε παραπάνω, η επιστημονική μέθοδος και η γνώση στην οποία καταλήγει έχει έναν έντονο αντικειμενικό χαρακτήρα υποβαθμίζοντας τη σημασία του υποκειμένου και του τρόπου που αυτό βιώνει τον κόσμο αλλά και την επιστημονική γνώση. Αυτή η μείωση της σημασίας του υποκειμένου στην επιστημονική μέθοδο έδωσε λαβή στο να καταγγελθεί για απομάγευση και απονέκρωση του κόσμου. Για το ότι αποτελεί μία ακριβή μεν ανατομία του κόσμου που όμως τελικά τον μετατρέπει σε ένα πτώμα άνευ ζωής, νοήματος  και προοπτικής. Επίσης, οδήγησε στη διατύπωση του παραδόξου του υποκειμένου από τον πατέρα της φαινομενολογικής σχολής και μαθηματικό Ε. Χούσερλ. Σύμφωνα με αυτό, ενώ η εξασκημένη υποκειμενική εμβίωση του κόσμου είναι απαραίτητη για την επιστημονική δημιουργία, την ίδια στιγμή η επιστήμη έτσι  όπως διαμορφώθηκε τους τελευταίους αιώνες δεν μπορεί να την τροφοδοτήσει, την υποβαθμίζει και εντέλει καταλήγει στην εξάλειψή της.  Πώς μπορούμε να υπερβούμε αυτό το παράδοξο και να ανοίξουμε νέους δρόμους υποκειμενοποίησης της επιστημονικής γνώσης;

Σε αυτό το ερώτημα μπορεί να συνεισφέρει η εμπλοκή της τέχνης. Η τέχνη ως μία κατεξοχήν κίνηση υποκειμενοποίησης και εμβάθυνσης της προσωπικής εμπειρίας, μπορεί να αλληλεπιδράσει με την επιστημονική γνώση και μέθοδο και με αυτόν τον τρόπο να οδηγήσει σε νέες αφομοιώσεις και θεωρήσεις που θα πυροδοτήσουν καινοτόμες επιστημονικές προσεγγίσεις. Αντίστροφα, η επιστήμη σε αυτή την αλληλεπίδραση μπορεί να προσφέρει στην τέχνη νέες «λέξεις» του κοσμικού λεξικού, δηλ. νέες όψεις της πραγματικότητας, αλλά και ρήξη με αυτονόητες κατανοήσεις και προκαταλήψεις. Με αυτόν τον τρόπο, οδηγεί σε διεύρυνση του υποκειμένου και κατά συνέπεια σε νέες καλλιτεχνικές αναζητήσεις και συλλήψεις. Αυτή η θετική ανάδραση επιστήμης και τέχνης συνοψίζεται σχηματικά στο Σχ. 1.

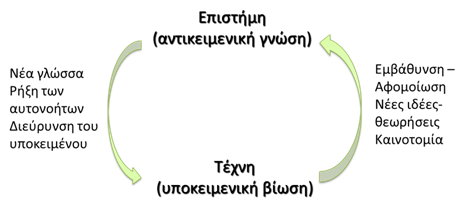
Σχήμα 1. Συνοπτική παρουσίαση της θετικής ανάδρασης μεταξύ επιστήμης και τέχνης με κύρια αφορμή το πρόβλημα της υποκειμενοποίησης της επιστημονικής γνώσης και μεθόδου.

Στις παραγράφους που ακολουθούν, θα εστιάσουμε στην φράκταλ ή μορφοκλασαμτική γεωμέτρια ως ένα παράδειγμα σύγχρονης αλληλεπίδρασης μεταξύ επιστήμης και τέχνης. Στην επόμενη παράγραφο ΙΙ, θα γίνει  μία σύντομη εισαγωγή στις βασικές έννοιες της φράκταλ γεωμετρίας και στην παράγραφο ΙΙΙ, θα αναφερθούμε στις αλληλεπιδράσεις της κυρίως με τη ζωγραφική και εντελώς ενδεικτικά και στοχευμένα με την ποίηση. Περιττό να τονίσουμε ότι σε καμιά περίπτωση, τα στοιχεία που θα παρατεθούν στην παράγραφο ΙΙΙ δεν εξαντλούν το θέμα της σχέσης φράκταλ γεωμετρίας και τέχνης.

ΙΙ. Φράκταλ γεωμετρία : Μία μικρή εισαγωγή

ΙΙ.1 Το παιχνίδι

Ας ξεκινήσουμε με ένα παιχνίδι που συνήθως ονομάζεται παιχνίδι του χάους (chaos game) αλλά θα μπορούσε να λέγεται και παιχνίδι των φράκταλς. Θεωρήστε ότι έχετε τρία μη συνευθειακά σημεία Α,Β,C σε ένα επίπεδο (βλ. σχ. 2).

Σχήμα 2. Το παιχνίδι του χάους

Στη συνέχεια διαλέξτε ένα τυχαίο σημείο στο επίπεδο (σημείο 1 στο σχ.2) και μετακινήστε το με βάση τους παρακάτω κανόνες:

1. Επιλέξτε τυχαία ένα από τα τρία μη συνευθειακά σημεία (έστω το C)
2. Μετακινήστε το σημείο 1 στο μέσο του ευθύγραμμου τμήματος με άκρα τα σημεία 1, C (σημείο 2 στο σχ.2).
3. Επαναλάβετε τα βήματα 1,2  ξεκινώντας τώρα από το σημείο 2 (σημεία 3,4,5).
4. Κρατήστε όλα τα σημεία της τροχιάς του αρχικού σημείου σημειωμένα στο επίπεδο.

Το ερώτημα του παιχνιδιού είναι να μαντέξτε τι σχήμα θα δώσουν τα σημεία της τροχιάς που προκύπτουν από την εφαρμογή των παραπάνω κανόνων; Είναι προφανές ότι το σημείο γρήγορα θα μπει στο εσωτερικό του τριγώνου ABC και θα παραμείνει εκεί για πάντα. Σχηματίζοντας όμως τι; Θα γεμίσει ομοιόμορφα αλλά άτακτα όλο το εσωτερικό του τριγώνου ή θα επαναλαμβάνεται σε συγκεκριμένα σημεία;  Τίποτα από τα δύο. Το τι σχήμα μας δίνουν τα σημεία της τροχιάς φαίνεται στο σχήμα 2 όπου δείχνονται τα  πρώτα 50 σημεία (σχ. 3α), στη συνέχεια τα 100 (σχ.3β) και τέλος τα σημεία των 1000 επαναλήψεων των κανόνων του παιχνιδιού (σχ. 2γ). Μη αναμενόμενα, η τροχιά δημιουργεί σιγά-σιγά ένα περίεργο σχήμα που θυμίζει τρίγωνο με την ιδιαιτερότητα όμως να γεμίζει το εσωτερικό του από σμικρυμένα αντίγραφα του εαυτού του σε όλο και μικρότερες κλίμακες.  Όπως φαίνεται στο σχ. 2δ, η αυτοομοιότητα είναι ακριβής και συνεχίζεται επ’άπειρον αν αφήσουμε την τροχιά να «τρέξει» για άπειρο χρόνο. Είναι σα να «κεντάει» η τροχιά το εσωτερικό του τριγώνου πηδώντας φαινομενικά τυχαία από σημείο σε διαφορετικό σημείο αλλά τελικά σχηματίζοντας αυτό το εντυπωσιακό κέντημα με μια αξιοθαύμαστη τάξη που χαρακτηρίζεται από τη συμμετρία της αυτοομοιότητας και όχι από τις γνωστές της μεταφοράς και περιστροφής.  Το παραγόμενο σχήμα ονομάζεται τρίγωνο του Sierprinski από το όνομα του Πολωνού μαθηματικού που πρώτος το ανακάλυψε.

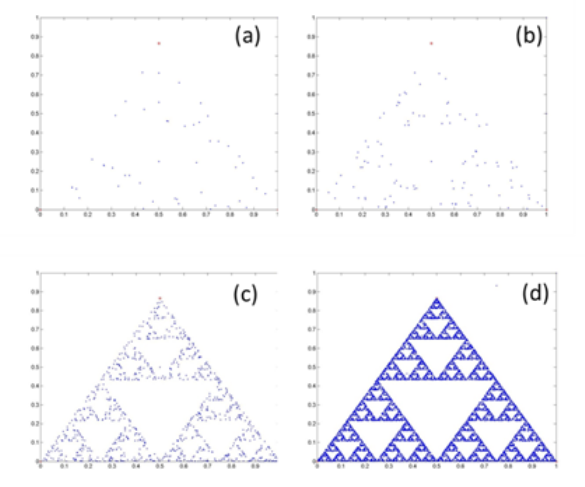
Σχήμα 3. Διάφορες φάσεις σχηματισμού του τριγώνου του Sierprinski με εφαρμογή των κανόνων του παιχνιδιού του χάους 50, 100, 1000 και 10000 φορές.

ΙΙ.2 Και τώρα η πραγματικότητα

Το τρίγωνο του Sierprinski είναι πράγματι εντυπωσιακό αλλά μήπως είναι απλώς μία ιδιαιτερότητα των μαθηματικών χωρίς αντίκρυσμα στον πραγματικό κόσμο που ζούμε; Όπως είπαμε, βασικό γνώρισμα του τριγώνου του SIerprinski  είναι η αυτοομοιότητα, οπότε το παραπάνω ερώτημα μεταφράζεται στο αν υπάρχει αυτοομοιότητα στη φύση και σε άλλες δομές. Η απάντηση δίνεται στο σχ. 4, όπου δείχνονται φυσικές δομές (ένα μπρόκολο (4α), ένα δένδρο (4β), μία αστραπή (4γ), μέρη του κυκλοφορικού συστήματος του αίματος (3δ, 3ε)), η οροσειρά των Άλπεων (3ζ) και η επιφάνεια πλατίνας μετρημένη με μικροσκόπιο ατομικής δύναμης (3η)) που εμφανίζουν χαρακτηριστικά αυτοομοιότητας αφού αποτελούνται από σμικρυμένα αντίγραφα του εαυτού τους. Φυσικά, η αυτοομοιότητα δεν είναι απόλυτα ακριβής και είναι στατιστικού τύπου, αλλά δεν μπορεί να παραθεωρηθεί αφού φαίνεται να αποτελεί κοινό χαρακτηριστικό πολλών μορφών που συναντάμε στα φυσικά και βιολογικά συστήματα. Η ευκλείδια γεωμετρία δεν φαίνεται ικανή να περιγράψει τέτοια αντικείμενα, οπότε δημιουργείται η ανάγκη για την θεμελίωση μιας νέας γεωμετρία που θα στοχεύει στην μαθηματική περιγραφή αυτών των αντικειμένων και θα βασίζεται στη συμμετρία της αυτοομοιότητας που αυτά επιδεικνύουν. Αυτή η γεωμετρία, είναι η γεωμετρία των φράκταλς και είναι το θέμα αυτού του άρθρου.

Σχήμα 4. Παραδείγματα φράκταλ μορφών που συναντάμε στη φύση

ΙΙ.3 Αρχή σοφίας επίσκεψη ονομάτων … και προσώπων

Ο όρος fractal προτάθηκε από τον Γάλλο μαθηματικό B. Mandelbrot θεμελιωτή της φράκταλ γεωμετρίας στο βιβλίο του «Les objects Fracals” (1977) και προέρχεται από το γαλλικό όρο fractus που σημαίνει ακανόνιστο, αποσπασματικό, σπασμένο και την κατάληξη al από το γνωστό αραβικό όρο algebra. Το σχετικό απόσπασμα από την αγγλική έκδοση του βιβλίου αναφέρει «“Many important spatial patterns of Nature are either irregular or fragmented to such an extreme degree that … classical geometry … is hardly of any help in describing their form. … I hope to show that it is possible in many cases to remedy this absence of geometric representation by using a family of shapes I propose to call fractals — or fractal sets.” [Mandelbrot, “Fractals,” 1977].

Η πρώτη ελληνική μετάφραση του όρου προτάθηκε από τον καθ. Στ. Πνευματικό και ήταν «μορφοκλασματικό». Ακολούθησαν και άλλες απόπειρες όπως κλασμίδιο ή κλασματίδιο.  Παρότι ο όρος μορφοκλασματικό είναι ετυμολογικά επιτυχής, το μεγάλο μήκος του και η εύκολη ελληνοποίηση της λέξης fractal στα ελληνικά ως φράκταλ, οδήγησε στην καθιέρωση του όρου φράκταλ στο μεγαλύτερο μέρος της ελληνικής βιβλιογραφίας.   Τον όρο αυτό θα χρησιμοποιήσουμε και σε αυτήν την εργασία.

Στην επόμενη παράγραφο, θα γίνει μία σύντομη περιγραφή των μαθηματικών που χρησιμοποιούνται στη φράκταλ γεωμετρία χωρίς να δώσουμε ιδιαίτερη έμφαση στην αυστηρή θεμελίωση, ενώ στην μεθεπόμενη παράγραφο ΙΙΙ θα ξεναγηθούμε στις εφαρμογές της φράκταλ γεωμετρίας και σκέψης σε διάφορες περιοχές όχι μόνο της επιστήμης αλλά και του πολιτισμού γενικότερα.

ΙΙ.4 Λίγα μαθηματικά

Ξεκινάμε με το να επαναλάβουμε ότι η φράκταλ γεωμετρία είναι ουσιαστικά η γεωμετρία των αυτοόμοιων δομών, αντικειμένων, μορφών, σχήματων και ακόμα διαδικασιών εξέλιξης στο χρόνο. Με τον όρο αυτοομοιότητα εννοούμε ότι η εν λόγω δομή παραμένει αναλλοίωτη σε μετασχηματισμό αλλαγής κλίμακας (scaling invariance).  Με άλλα λόγια, η φραάκταλ γεωμετρία είναι η γεωματρία της συμμετρίας της αυτοομοιότητας.  Και επειδή μία τυπική λύση μιάς εξίσωσης αυτοομοιότητας είναι μία συνάρτηση που εκφράζεται ως νόμος δύναμης (αυτό το αφήνουμε για άσκηση), συχνά η μαθηματική έκφραση της παρουσίας αυτοομοιότητας είναι ένας νόμος δύναμης ως προς την μεταβλητή της  κλίμακας μελέτης. Ο νόμος δύναμης χαρακτηρίζεται από έναν εκθέτη που ουσιαστικά καθορίζει την ποσοτική συμπεριφορά του και σχετίζεται με την διάσταση φράκταλ της εξεταζομένης δομής η οποία σε αντίθεση με τη συνηθισμένη ευκλείδια διάσταση δεν περιορίζεται σε ακέραιες τιμές. Κατά συνέπεια, μπορεί να υποστηριχθεί ότι οι έννοιες-κλειδιά στη φράκταλ γεωμετρία είναι η αυτοομοιότητα, ο νόμος δύναμης και η φράκταλ μη-ακέραια  διάσταση.

Για να κατανοηθούν καλύτερα αυτές οι έννοιες και οι μεταξύ τους διασυνδέσεις, ας αναρωτηθούμε αρχικά τι είναι αυτοομοιότητα. Είναι κάτι ιδιαίτερο και σπάνιο ή μήπως υπάρχει και στα συνηθισμένα σχήματα της σχολικής γεωμετρίας μας;

Αν θεωρήσουμε ένα ευθύγραμμο τμήμα θα διαπιστώσουμε ότι αποτελείται από σμικυμένα αντίγραφα του εαυτού του και αυτά πάλι από σμικρυμένα αντίγραφά τους κ.ο.κ. Το ίδιο και με ένα τετράγωνο στις δύο διαστάσεις  και  έναν κύβο στις 3 ή Ν διαστάσεις. Δηλ. η αυτοομοιότητα είναι μία κοινή ιδιότητα των βασικών ευκλείδιων σχημάτων.

Για να την ποσοτικοποιήσουμε αρκεί να ρωτήσουμε από πόσα σμικρυμένα αντίγραφα του γραμμικής διάστασης ε  αποτελείται ένα ευθύγραμμο τμήμα μήκους 1. Η απάντηση είναι απλή και είναι Ν(ε)=ε^-1. Για το τετράγωνο το πλήθος αυτό γίνεται Ν(ε)=ε^-2 και για κύβο Ν στις δ διαστάσεις Ν(ε)=ε^–d. Βλέπουμε δηλ. ότι το πλήθος των σμικρυμένων αντιγράφων που απαιτούνται για την κάλυψη του κύβου δίνεται από ένα νόμο δύναμης με εκθέτη την αρνητική διάσταση του αντικειμένου. Οπότε με τη βοήθεια της αυτοόμοιας ανάλυσης οδηγούμαστε σε έναν αλγεβρικό ορισμό της διάστασης:

(1)

όπου ε είναι η κλίμακα εξέτασης του αντικειμένου και Ν(ε) είναι αριθμός των αντιγράφων του σε αυτή την κλίμακα. Για να αποφύγουμε προβλήματα επίδρασης του πεπερασμένου μεγέθους των αντικειμένων ως προς την θεωρούμενη κλίμακα γράφουμε την (1) ως:

          (2)

Υπενθυμίζουμε ότι στην περίπτωση του ευθύγραμμου τμήματος η (2) δίνει d=1, για το τετράγωνο  d=2 ενώ για κύβο παίρνουμε d=3. Όμως η σχέση αυτήμπορεί να εφαρμοστεί σε κάθε περίπτωση σχήματος με αυτοόμοια χαρακτηριστικά και επομένως και για το τρίγωνο του Sierprinski που προκύπτει από το παιχνίδι του χάους και με το οποίο ξεκινήσαμε στην εισαγωγή του άρθρου μας; Σε κάθε κλίμακα ανάλυσής του, το τρίγωνο του Sierprinski αποτελείται από τρία σμικρυμένα αντίγραφα του εαυτού του καθένα από το οποίο έχει πλευρά το ½ του αρχικού. Έτσι αν θεωρήσουμε ότι το αρχικό τρίγωνο έχει πλευρά μήκους 1, στη μεγαλύτερη κλίμακα αυτοομοιότητας αποτελείται από 3 όμοια τρίγωνα σμικρυμενα 50%, δηλ. με πλευρά ½. Το ίδιο αν το τρίγωνο εξετασθεί στην k-ιοστή κλίμακα αποτελέιται από N(ε)=3^k τρίγωνα με πλευρά ε=2^–k (επαληθεύστε το!). Εφαρμόζοντας τώρα τη φόρμουλα (2) προκύπτει ότι:

Δηλαδή η διάσταση του τριγώνου του Sierprinski υπολογιζόμενη ακριβώς όπως αυτή του ευθύγραμμου τμήματος και του τετραγώνου προκύπτει μη ακέραιος και μάλιστα άρρητος αριθμός!! Ο αριθμός αυτός είναι μεταξύ του 1 και του 2 όπως αναμένεται αφού το τρίγωνο του Sierprinski ζει στο επίπεδο αλλά δεν καλύπτει με συνεχή τρόπο ένα μέρος του. Είναι δηλαδή ένα αμφίβιο μεταξύ του μονοδιάστατου και διδιάστατου χώρου με τη διάστασή του να δηλώνει ουσιαστικά την εγγύτητα του προς τον ένα ή άλλο χώρο.

Εκτός από το τρίγωνο του Sierprinski και τις άλλες γνωστές φράκταλ δομές που εμφανίζουν αυστηρή αυτοομοιότητα σε όλες τις κλίμακες (σύνολο Καντόρ, καμπύλη του Κώχ), υπάρχουν σύνολα που παράγονται με εξίσου απλούς τρόπους επανάληψης απλών κανόνων που χαρακτηρίζονται από προσεγγιστική αυτό-ομοιότητα που επιτρέπει την εμφάνιση νέων μορφών με εκπληκτική πολυπλοκότητας όλες τις κλίμακες ανάλυσης.  Κλασικό παράδειγμα και ένα από τα πιο αναγνωρίσιμα φράκταλς είναι το σύνολο του Μάντελμπροτ (Σχ. 5). Δημιουργείται στο επίπεδο των μιγαδικών αριθμών από εκείνα τα μιγαδικά c για τα οποία η επανάληψη άπειρες φορές της σχέσης z_n+1=z­­_n²+c για z_o=0 οδηγεί σε πεπερασμένο z. Τα σημεία με συντεταγμένες το πραγματικό και φανταστικό μέρος αυτών των c, σημειώνονται με μαύρο στην αναπαράσταση του συνόλου. Τα υπόλοιπα σημεία χρωματίζονται ανάλογα με τον ρυθμό που οι επαναλήψεις της παραπάνω σχέσης οδηγούν στο άπειρο. Ο μορφολογικός πλούτος και η ανεξάντλητη αισθητική ομορφιά του συνόλου, το έχει καταστήσει ένα από τα δημοφιλέστερα μαθηματικά αντικείμενα που δείχνει ότι εκτός από τη φύση και τα μαθηματικά έχουν κρυμμένες εκπλήξεις που περιμένουν να τις συναντήσουμε.

Σχήμα 5. Το σύνολο του Μάντελμπροτ συνολικά (πάνω δεξιά) και σε διάφορες μεγεθύνσεις του.

ΙII. Η φράκταλ γεωμετρία στην τέχνη

Η φράκταλ γεωμετρία έδειξε με τον πιο εμφανή τρόπο την μορφολογική πολυπλοκότητα που μπορούν να έχουν απλές μαθηματικές σχέσεις. Ουσιαστικά, πρόσθεσε μία νέα διάσταση στη σχέση μεταξύ μαθηματικών και μορφής. Αυτό, φυσικά, δεν μπορούσε να αφήσει αδιάφορη την τέχνη στην οποία το πρόβλημα της μορφής είναι κεντρικής σημασίας. Επίσης, μετά την διατύπωση της φράκταλ γεωμετρίας διαπιστώθηκε ότι αρκετά έργα τέχνης παλαιότερα αυτής της διατύπωσης έχουν φράκταλ χαρακτηριστικά. Η φράκταλ γεωμετρία έχει επηρεάσει σχεδόν όλους τους τομείς της τέχνης.  Εδώ, για λόγους οικονομίας χώρου, θα περιοριστούμε στη ζωγραφική και την ποίηση αφήνοντας την αναφορά στις υπόλοιπες τέχνες για επόμενη εργασία. Σε κάθε τέχνη, θα ξεκινάμε από αρχαιότερα της φράκταλ γεωμετρίας έργα τέχνης με φράκταλ χαρακτηριστικά (προ-φράκταλ έργα) και θα περνάμε στη συνέχεια σε σύγχρονα έργα που έχουν επηρεαστεί από αυτή (μετα-φράκταλ έργα).

III.1 Ζωγραφική

ΙΙΙ.1.Α Προ-φράκταλ έργα ζωγραφικής με φράκταλ χαρακτηριστικά

Θα ξεκινήσουμε με το τρίγωνο του Sierpinski με το οποίο ξεκινήσαμε και την αναφορά μας στη φράκταλ γεωμετρία. Το μοτίβο του μέχρι τη δεύτερη ή και τρίτη επανάληψη συναντάται στα δάπεδα αρκετών εκκλησιών και αρχοντικών οικείων του όψιμου μεσαίωνα και της Αναγέννησης. Ένα αντιπροσωπευτικό παράδειγμα είναι το δάπεδο του καθεδρικού του Anangi που κατασκευάσθηκε το 1100 μ.Χ. και δείχνεται στο σχ. 6α. Να σημειωθεί ότι τα τρίγωνα του δαπέδου είναι καμπύλα, προκαλώντας τον περίεργο αναγνώστη να εξετάσει την επέκταση του τριγώνου του Sierprinski σε καμπύλα τρίγωνα και άλλα πολύγωνα. Συμπληρωματικά, στο σχ.6β παρουσιάζεται μία εικόνα από ένα εκκλησιαστικό χειρόγραφο του 12^ου αιώνα από τη Μ. Βρετανία στο οποίο δείχνεται ο Χριστός καθώς αρχιτεκτονεί τον κόσμο. Είναι εντυπωσιακό ότι ο άγνωστος καλλιτέχνης, απεικόνισε με μία σχεδόν φράκταλ γραμμή το όριο των υδάτων τη στιγμή που αυτά συνάζονται την Τρίτη ημέρα της δημιουργίας και από μέσα τους αναδύεται η γη.

Σχήμα 6. Μέρος του δαπέδου του καθεδρικού ναού του Anangi (α) με το μοτίβο του τριγώνου του Sieprinski και εικόνα από χειρόγραφο του 12ου αιώνα με τον Χριστό ως δημιουργό του κόσμου.

Γενικότερα, η μορφή των στροβιλισμών του νερού αποτέλεσε πρόκληση για πολλούς ζωγράφους λόγω της γοητευτικής πολυπλοκότητάς τους και τους οδήγησε να χρησιμοποιήσουν αυτοόμοιες δομές πολύ κοντά σε αυτές που σήμερα ονομάζουμε φράκταλ μορφές. Έτσι ο Λεονάρντο Ντα Βίντσι σχεδιάζει τους στροβιλισμούς του νερού που εισέρχεται σε μία δεξαμενή και προσπαθεί να απεικονίσει την αυτοομοιότητα που αυτοί έχουν (σχ. 7α), ενώ ο Ιάπωνας Κοτσουσίκα Χοκουσάι στο γνωστό του Κύμα ζωγραφίζει την άκρη του κύματος με τρόπο που παραπέμπει στην καμπύλη του Koch, ένα από τα τυπικά παραδείγματα φράκταλ καμπύλης (σχ. 7β). Το ίδιο και όταν ζωγραφίζει έναν καταρράκτη που «σπάει» σε μικρότερους καταρράκτες, όπου οι διακλαδώσεις θυμίζουν φράκταλ διακλαδώσεις με πολύ καλή αυτοομοιότητα (σχ. 7β).

Σχήμα 7. Σχέδιο του Ντα Βίντσι με τους στροβιλισμούς του νερού όταν χύνεται σε μία δεξαμενή (σχ.6α) και έργα του Χοκουσάι με φράκταλ κύματα και διακλαδώσεις καταρρακτών (6β).

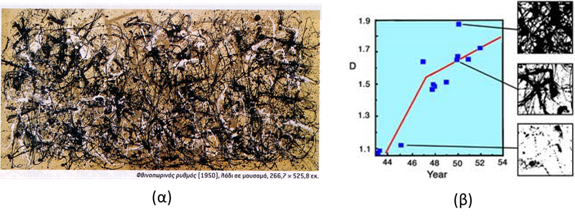
Σχήμα 8. α) Το έργο του Πόλλοκ Φθινοπωρινός ρυθμός του 1950 κατασκευασμένο με την τεχνική του dripping που επινόησε ο Πόλλοκ και β) η φράκταλ διάσταση των έργων του υπολογισμένη από την ανάλυση της ομάδας του Τέιλορ σε διάγραμμα συναρτήσει του χρόνου κατασκευής του έργου. Δείχνεται καθαρή αυξητική τάση που χαρακτηρίζει την εξέλιξη του ζωγράφου.

Ιδιαίτερη περίπτωση στη φράκταλ ζωγραφική αποτελεί ο Αμερικανός εξπρεσιονιστής Τζάκσον Πόλλοκ (1912-1956). Χωρίς τα έργα του να αναπαριστούν φυσικές μορφές και δημιουργημένα με την τεχνική του dripping που ανήκει στη γενικότερη κατηγορία τουaction painting, επιδεικνύουν φράκταλ χαρακτηριστικά όπως έδειξαν σχετικές μελέτες της ομάδας του Ρίτσαρντ Τεϊλορ από το Πανεπιστήμιο New South Wales της Αυστραλίας. Στο σχ. 8α φαίνεται το έργο του Φθινοπωρινός ρυθμός (1950), ενώ στο σχ.8β δείχνεται ένα αποτέλεσμα της ανάλυσης της ομάδας του Τέιλορ για την εξέλιξη της φράκταλ διάστασης των έργων του Πόλλοκ με το χρόνο κατασκευής τους.

ΙΙΙ.1.Β Μετά-φράκταλ έργα ζωγραφικής : αντί για πινέλα, εξισώσεις

Όπως αναφέραμε παραπάνω, τα φράκταλς έδειξαν με τον πλέον εναργή τρόπο ότι τα μαθηματικά υποβοηθούμενα από σχετικούς αλγόριθμους και γραφικά μπορούν να δημιουργήσουν ένα απεριόριστο φάσμα μορφών και σχημάτων. Κατά συνέπεια, μπορούν να χρησιμοποιηθούν αντί για τα πινέλα του ζωγράφου και ουσιαστικά να συστήσουν μία νέα προσέγγιση στη ζωγραφική. Παρακάτω θα δώσουμε κάποια παραδείγματα έργων που κατασκευάσθηκαν σε αυτή την προσέγγιση αν και πιστεύουμε ότι χρειάζεται ακόμη αρκετή εμβάθυνση και προσπάθεια για να ωριμάσει η προσέγγιση αυτή και να βοηθήσει τη θετική ανάδραση μεταξύ επιστήμης και τέχνης όπως την περιγράψαμε στην εισαγωγή του άρθρου μας.

Για την δημιουργία φράκταλ έργων χρησιμοποιήθηκαν πολλές μαθηματικές διεργασίες που μπορούν να καταλήξουν στον σχηματισμό φράκταλ μορφών όπως επαναλαμβανόμενα συστήματα συναρτήσεων, καμπύλες που γεμίζουν το χώρο, δυναμικά συστήματα με παράξενους ελκυστές, αλγόριθμοι που κατασκευάζουν φράκταλ τοπία, μέθοδοι επίλυσης μη γραμμικών εξισώσεων κλπ.   που υλοποιούν με πιθανοκρατικό τρόπο κανόνες μετασχηματισμού στο επίπεδο ή τον χώρο παρόμοια με το παιχνίδι του χάους αλλά με περισσότερες παραμέτρους.  Δύο παραδείγματα έργων που έχουν δημιουργηθεί με επαναλαμβανόμενα συστήματα συναρτήσεων δείχνονται στο σχ.9, ενώ στα σχ. 10 και 11 παρουσιάζονται έργα που προέκυψαν από καμπύλες που γεμίζουν το χώρο σε συνδυασμό με τα γνωστά έργα τέχνης του Λεονάρντο Ντα Βίντσι «Μόνα Λίζα» (σχ. 10) και «Ο άνθρωπος του Βιτρούβιου» (σχ. 11). Το έργο του σχ. 11 τιτλοφορείται Ο μορφοκλασματικός άνθρωπος και ο περίγραμμα του προέρχεται από το σχέδιο του ντα Βίντσι «Ο άνθρωπος του Βιτρουβίου» που αποτελεί μία σπουδή στις εξωτερικές συμμετρίες και αναλογίες του ανθρωπίνου σώματος. Η σχεδόν μορφοκλασματική γραμμή που γεμίζει μη τεμνόμενη το περίγραμμα είναι μία προσπάθεια να αποδοθεί η σχεδόν μορφοκλασματική δομή και λειτουργία των εσωτερικών ιστών και οργάνων του σώματος και κατά προέκταση της συνείδησης του ανθρώπου. Επίσης, το όλο εγχείρημα υποκινείται από τη διερώτηση για την ενότητα  του ανθρωπίνου  σώματος και διερευνά την πιθανότητα ενός απεντοπισμένου ενοποιού «κέντρου» που διατρέχει όλη την έκτασή του ανθρώπου.

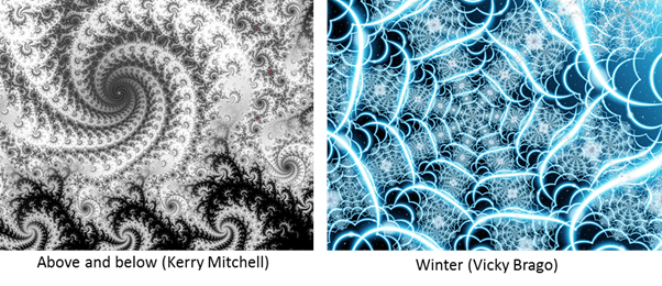
Σχήμα 9. Φράκταλ ψηφιακά έργα κατασκευασμένα με την τεχνική των επαναλαμβανόμενων συστημάτων συναρτήσεων.

Σχήμα 10. Η Μόνα Λίζα του Ντα Βίντσι και ο σχηματισμός του αινιγματικού χαμόγελού της με μία φράκταλ καμπύλη κάλυψης του επιπέδου.

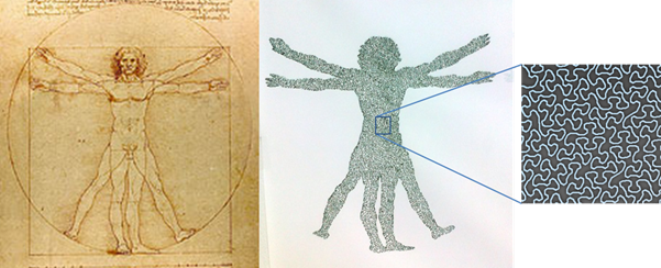
Σχήμα 11. Ο άνθρωπος του Βιτρούβιου του Ντα Βίντσι μαζί με την πλήρωση του περιγράμματός του από μία καμπύλη κάλυψης του επιπέδου (Ο μορφοκλασματικός άνθρωπος, Β. Κωνσταντούδης 2011).

ΙΙΙ.2 Ποίηση

ΙΙΙ.2.Α Προ-φράκταλ ποιήματα με φράκταλ χαρακτηριστικά

Η γνωστή Αμερικανίδα ψυχολόγος και κριτικός της τέχνης L. Pollard-Gott, L. Στο άρθρο της “Fractal repetition in the poetry of Wallace Stevens,” Language and Style 19 (1989), 233-249, υποστήριξε ότι στο ποίημα του Steven Wallace “ The Sail of Ulysses” οι λέξεις με ρίζα το Know διασπείρονται με ιεραρχικό τρόπο που έχει τη φράκταλ δομή του συνόλου Καντόρ (σχ. 12). Αιτιολόγησε το εύρημά της αυτό με το επιχείρημα ότι πιθανώς ο Wallace έστω και ασυνείδητα διάρθρωσε το ποίημά του με τον ιεραρχικό τρόπο που παρατηρείται συχνά στη φύση και στη μουσική. Αρκετές μελέτες έκτοτε έδειξαν ότι όχι μόνο σε ποιήματα αλλά και σε κάθε κείμενο οι σημαντικές λέξεις που το νοηματοδοτούν είναι διασκορπισμένες με έναν φράκταλ ιεραρχικό τρόπο που μπορεί να ποσοτικοποιηθεί με τη φράκταλ διάσταση. Αυτή η φράκταλ διασπορά των σημαντικών λέξεων δεν είναι συνειδητή και αποτελεί το ποσοτικό ίχνος του νοήματος του κειμένου. Αυτό που ενδεχομένως κάνουν οι ποιητές είναι να χειρίζονται αυτό το χαρακτηριστικό με τον καλύτερο δυνατό τρόπο και να ρυθμίζουν την βαρύτητα της κάθε λέξης στα ποιήματα τους αξιοποιώντας το, όπως ακριβώς έκανε ο Wallace στο παραπάνω ποίημα.

________________________________________________________________________________ Σχήμα 12. Το ποίημα του S. Wallace και η δομή Καντόρ των λέξεων με ρίζα Know.

ΙΙΙ.2.Β Μετα-φράκταλ ποιήματα

Αυτά μπορεί να είναι είτε ποιήματα που ενσωματώνουν μέσα τους φράκταλ δομές με πιο συνειδητό τρόπο από αυτόν που αναφέραμε παραπάνω ή ποιήματα που αναφέρονται στη φράκταλ γεωμετρία ή σε φράκταλ δομές και αντικείμενα. Πολύ ενδεικτικά και μόνο για τη δεύτερη κατηγορία θα παρουσιάσουμε ένα ποίημα του Raymond Lucas γραμμένο το 2012 με τον τίτλο Taken There

TAKEN THERE

A curve that fills a plane
A plane that holds some space
Some space outstretched through time
A point reiterated indefinitely

Seen and misunderstood
Fractal dimensions
One inside another
One containing the others

Iteration piled high
And all the way down
Illogical conclusions
In logical delusions

Again and again
For good measure and scale
One again until the end
And then perhaps again

Και θα κλείσουμε αυτήν την εξαιρετικά σύντομη και ενδεικτική αναφορά στην σχέση της φράκταλ γεωμετρίας με την ποιητική δημιουργία, με την παράθεση ενός σχετικού χαϊκού με αφορμή μία φωτογραφία που φαίνεται μαζί με το ποίημα στο σχ. 13.

Σχήμα 13. Φωτογραφία κλαδιών δένδρου μαζί με χαϊκού ποίημα που εμπνέεται από την φράκταλ δομή τους

* Ο Βασίλης Κωνσταντούδης είναι δρ. φυσικός και εργάζεται στο Ινστιτούτο Νανοεπιστήμης και Νανοτεχνολογίας, ΕΚΕΦΕ Δημόκριτος. Κυρίως ασχολείται με μαθηματικά και υπολογιστικά προβλήματα που αναδύονται στη νανομετρολογία δηλ. στην προσπάθειά μας να μετρήσουμε πολύ-πολύ μικρά πραγματάκια που φτιάχνουμε στη νανοτεχνολογία. Αρκετές φορές αυτά έχουν πολύπλοκη μορφολογία και για να τα περιγράψει έχει αφιερώσει αρκετές ώρες στην προσπάθεια να εξοικειωθεί με μεθόδους της στοχαστικής ανάλυσης και της φράκταλ γεωμετρίας. Όταν κουράζεται ή απελπίζεται, του αρέσει να σηκώνει το κεφάλι του από το γραφείο και τον υπολογιστή και να κοιτάει έξω από το παράθυρο.