Fractal
Home / ΕΠΙΣΤΗΜΕΣ / Fractal. Τέχνες και επιστήμες μαζί.
11/07/2014, 1:14 μμ

Fractal. Τέχνες και επιστήμες μαζί.

του Μιχάλη Παναγόπουλου // *

 

fractal 1Στο άκουσμα της λέξης φράκταλ (σ΄ ελληνική απόδοση μορφόκλασμα) οι σκέψεις και τα συναισθήματα, που μπορεί να δημιουργηθούν σε κάποιον εξαρτώνται, σε μεγάλο βαθμό, από το μορφωτικό του υπόβαθρο και τα επαγγελματικά ή ερασιτεχνικά του ενδιαφέροντα. Ένας μαθηματικός ή κάποιος τεχνοκράτης θα ισχυριστούν ότι ο όρος φράκταλ είναι ένας καθαρά μαθηματικός όρος. Αντίθετα, ένας καλλιτέχνης, ενδεχομένως , θα πει ότι φράκταλ είναι μια παράξενη γεωμετρική κατασκευή , που προσφέρει περίεργα, ιδιαίτερα και ενδιαφέροντα σχήματα για καλλιτεχνική έκφραση. Κάποιος που απλά έχει ακουστά τη λέξη, συνδέει τα φράκταλ με εντυπωσιακά σχήματα, που σχετίζονται με «βαριά» μαθηματικά και πολύπλοκες χαοτικές θεωρίες (το γνωστό πέταγμα πεταλούδας που προκαλεί καταιγίδες κτλ).

Τι ακριβώς είναι;

Για να καταλάβει κάποιος τι πραγματικά είναι το φράκταλ πρέπει πρώτα -πρώτα να κατανοήσει τα δύο βασικότερα χαρακτηριστικά του (πρακτικά είναι αλληλένδετα μεταξύ τους). Την αυτοομοιότητα και τη μη ακέραια διάσταση. Αυτοομοιότητα είναι η ιδιότητα την οποία έχουν ορισμένα σχήματα να παρουσιάζουν την ίδια (ή σχεδόν την ίδια) δομή σε διαφορετικές κλίμακες. Ένα χαρακτηριστικό παράδειγμα αυτοομοιότητας είναι οι χάρτες των ακτογραμμών (για παράδειγμα της Βρετανίας , επειδή από εκεί τέθηκε πρώτη φορά το ερώτημα για τον ακριβή υπολογισμό του μήκους των ακτογραμμών της από τον μετεωρολόγο Fry Richardson!). Εκεί παρατηρούμε παρόμοια οφιοειδή μορφή της ακτογραμμής σε κάθε δυνατή κλίμακα. Κάθε φορά που «ζουμάρουμε» σε κάποιον κόλπο εμφανίζονται νέες λεπτομέρειες,  που δεν υπήρχαν σε μικρότερες κλίμακες, επομένως για να υπολογιστεί με ακρίβεια το μήκος της ακτογραμμής θα πρέπει να φτάσουμε στο επίπεδο του κόκκου της άμμου!

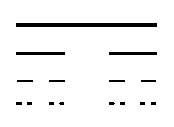
Σχήμα 1

Σχήμα 1

s2

Σχήμα 2

Πιο πιστές στην αυτοομοιότητα περιπτώσεις είναι η «σκόνη Cantor» και η καμπύλη Van Koch. Η πρώτη δημιουργείται όταν χωρίζουμε ένα ευθύγραμμο τμήμα σε τρία ίσα μέρη, αφαιρούμε το μεσαίο και επαναλαμβάνουμε διαδοχικά την διαδικασία  επ’ άπειρον στα εναπομείναντα τμήματα (Σχ. 1).

Η καμπύλη Van Koch δημιουργείται όταν χωρίσουμε και πάλι ένα ευθύγραμμο τμήμα σε τρία ίσα μέρη, αυτή τη φορά, όμως , στη θέση του κεντρικού τμήματος τοποθετούμε δύο τμήματα, ιδίου μήκους με το κεντρικό , ώστε να σχηματιστεί ένα είδος ισόπλευρου τριγώνου (Σχ. 2). Η αυτοομοιότητα είναι ξεκάθαρη καθώς αλλάζουμε κλίμακα και επαναλαμβάνεται η διαδικασία άπειρες φορές.

Οι καμπύλες αυτές μας βοηθούν να κατανοήσουμε και την άλλη περίεργη ιδιότητα των φράκταλ, δηλαδή τη μη ακέραια διάσταση.

Ας θυμηθούμε κάποια βασικά στοιχεία από τα σχολικά μας χρόνια. Ένα σχήμα,  που έχει μήκος και πλάτος και καλύπτει ένα εμβαδό είναι δισδιάστατο , επειδή ακριβώς έχει αυτές τις δύο διαστάσεις (μήκος, πλάτος), ενώ όταν υπάρχει και βάθος, τότε έχουμε τα τρισδιάστατα σχήματα. Μια καμπύλη ,όμως , δεν έχει πλάτος και για τον λόγο αυτό είναι μονοδιάστατη. Το σημείο δεν έχει διαστάσεις. Τι γίνεται ,όμως,  με την καμπύλη Van Koch; Είναι ξεκάθαρο ότι είναι «κάτι παραπάνω» από καμπύλη, αφού γεμίζει περισσότερο τον χώρο όσο πιο πολύ μεγεθύνουμε την κλίμακα (το μήκος της συνεχώς αυξάνεται!), αλλά και κάτι λιγότερο από δισδιάστατο σχήμα αφού δεν έχει πλάτος!

Εδώ ακριβώς είναι η συμβολή του γάλλου μαθηματικού Benoit Mandelbrot (πατέρας των φράκταλ), ο οποίος όρισε τη μη ακέραια διάσταση, δηλαδή διαστάσεις όπως το 1,58 (για την βρετανική ακτογραμμή) , που δείχνουν ακριβώς ότι έχουμε κάτι ενδιάμεσο μεταξύ των μονοδιάστατων και των δισδιάστατων σχημάτων. Αυτά τα σχήματα τα ονόμασε φράκταλς από την λατινική λέξη fractus (ή fractio) που σημαίνει σπασμένο, κομματιασμένο και την διάστασή τους διάσταση φράκταλ, η οποία δείχνει το πόσο «γεμίζει τον χώρο» η καμπύλη.

Χάος και φράκταλ

Σχήμα 3

Σχήμα 3

Η παράξενη ομορφιά τους σχετίζεται με την αιώνια γοητεία,  που πάντα ασκούσε στον άνθρωπο το άπειρο και το απειροστό. Όλα τα μαγευτικά παράδοξα,  που απασχόλησαν τις επιστήμες και την φιλοσοφία σχετίζονταν με τον ένα ή με τον άλλο τρόπο με την έννοια του απείρου. Έτσι και με τα φράκταλ βλέπουμε ότι όλες οι μη κανονικότητες εκκινούν από τις άπειρες διαδοχικές μεγεθύνσεις.

Η μεγάλη απήχηση, όμως, που απέκτησαν τα φράκταλ από τη δεκαετία του 1980 και μετά σχετίζεται με τα εντυπωσιακά σχήματα που δημιουργήθηκαν με την απεικόνιση της γοητευτικής χαοτικής θεωρίας. Χαοτικά είναι εκείνα τα φαινόμενα στα οποία πολύ μικρές αλλαγές στις αρχικές συνθήκες δίνουν τελείως διαφορετικά αποτελέσματα.

Ένα απλό παράδειγμα, που θα βοηθούσε στην κατανόηση αυτής της διατύπωσης είναι το ταξίδι Αθήνα – Θεσσαλονίκη με αυτοκίνητο. Η αρχική μας συνθήκη είναι το σημείο εκκίνησης του ταξιδιού (π.χ. η θέση στάθμευσης του αυτοκινήτου) για υπολογίζουμε τον συνολικό χρόνο του ταξιδιού μέχρι τη Θεσσαλονίκη.

Για τον ίδιο οδηγό, όχημα και συνθήκες ταξιδιού, μια αμελητέα αλλαγή στις αρχικές συνθήκες θα μπορούσε να φέρει τρομακτική αλλαγή στο τελικό αποτέλεσμα. Έτσι ας υποθέσουμε ότι ο οδηγός έχει παρκάρει το αυτοκίνητό του ελάχιστα μέτρα μακρύτερα από μια αρχική δεδομένη θέση. Θεωρητικά αυτό, από μόνο του, δεν θα έπρεπε να έχει καμία επίπτωση στη διάρκεια του ταξιδιού. Αν όμως στη νέα θέση,  που ήταν σταθμευμένο το όχημα έχει σπάσει , για παράδειγμα , ένας αγωγός ύδρευσης ,τότε μπορεί να προκληθεί τεράστια καθυστέρηση στην εκκίνηση του ταξιδιού. Ακόμη και να ακυρωθεί ! Οι  συνέπειες αυτής της καθυστέρησης είναι τελείως απρόβλεπτες και μπορεί να οδηγήσουν σε εντελώς διαφορετικά αποτελέσματα. Γι’ αυτό άλλωστε είναι και αδύνατη η πρόβλεψη φαινομένων,  που εξαρτώνται από πολλές παραμέτρους. Όπως η μετεωρολογική πρόβλεψη πέραν των λίγων ημερών.

Τέτοια χαοτικά φαινόμενα συμβαίνουν και στην επίλυση απλών μιγαδικών εξισώσεων και για αυτό κάποιοι επιστήμονες προσπάθησαν να δουν για ποιες τιμές των μεταβλητών έχουμε χαοτική (δηλαδή απρόβλεπτη) συμπεριφορά και για ποιες όχι.

Υπάρχουν τιμές μεταβλητών, που βρίσκονται σε όρια. Ανήκουν στη μία ή στην άλλη κατηγορία και η γραφική απεικόνιση του συνόλου αυτών των τιμών (π.χ. σύνολα Julia από τον μαθηματικό Gaston Julia) δίνει τα διάσημα και άκρως εντυπωσιακά φράκταλ σχήματα (Σχ. 3).

Σχήμα 4

Σχήμα 4

Το γνωστότερο όλων είναι το φράκταλ του συνόλου Mandelbrot (Σχ. 4), το οποίο έγινε δυνατό να αναπαρασταθεί λόγω της εξέλιξης των υπολογιστών τις τελευταίες δεκαετίες.

Η δύναμη των φράκταλ εντοπίζεται στη δυνατότητα να συνδυάζουν πολλά εντυπωσιακά πράγματα ταυτόχρονα. Περιγράφουν τις τόσο παράξενες χαοτικές συμπεριφορές, χαρακτηρίζονται από αυτοομοιότητα, έχουν μη ακέραια διάσταση. Παραλλήλως είναι πανέμορφα και αποδίδουν σουρεαλιστικές μορφές , που δεν μπορούσαμε να φανταστούμε, ανοίγοντας νέους δρόμους στις επιστήμες και στις τέχνες.

Είναι συγκλονιστική η ποικιλία που μπορεί να συναντήσει κάποιος τα φράκταλ και το πόσες εφαρμογές έχουν. Στη φύση φράκταλ δομή έχουν οι πνεύμονες και τα νεφρά μας, τα φύλλα πολλών δέντρων, κάποια είδη μπρόκολων, οι κεραυνοί, οι οροσειρές, ενώ εφαρμογές υπάρχουν και στην βιολογία, την γεωλογία αλλά και σε άλλες επιστήμες όπως η πληροφορική, η μετεωρολογία, η φυσική, η νευροψυχολογία κ.α. Τέλος, τα φράκταλ αποτελούν πηγή έμπνευσης για την conceptual art (εννοιακή τέχνη) και έχουν πολλές εφαρμογές στην εικονική πραγματικότητα και το animation.

Αυτός είναι άλλωστε και ο λόγος που τα φράκταλ θεωρούνται από τα πιο χαρακτηριστικά παραδείγματα συνταιριάσματος τέχνης και μαθηματικών, θεωρίας και εφαρμογής, ομορφιάς και συνέπειας της γεωμετρίας με την αισθητική και το αφηρημένο, της φιλοσοφίας με την έμπνευση. Είναι οι τέχνες και οι επιστήμες μαζί.

.

* Ο Μιχάλης Παναγόπουλος είναι Λέκτορας στο Τμήμα Τεχνών Ήχου & Εικόνας του Ιονίου Πανεπιστημίου.

 

  • Μοιραστείτε το άρθρο:
Ετικέτες:
ΣΧΕΤΙΚΑ ΑΡΘΡΑ

Back to Top